使用 NumPy 进行数组编程
前言
人们有时会说,与C++这种低级语言相比,Python以运行速度为代价改善了开发时间和效率。幸运的是,有一些方法可以在不牺牲易用性的情况下加速Python中的操作运行时。适用于快速数值运算的一个选项是NumPy,它当之无愧地将自己称为使用Python进行科学计算的基本软件包。
当然,很少有人将50微秒(百万分之五十秒)的东西归类为“慢”。然而,计算机可能会有所不同。运行50微秒(50微秒)的运行时属于微执行领域,可以松散地定义为运行时间在1微秒和1毫秒之间的运算。
为什么速度很重要?微观性能值得监控的原因是运行时的小差异会随着重复的函数调用而放大:增量50μs的开销,重复超过100万次函数调用,转换为50秒的增量运行时间。
在计算方面,实际上有三个概念为NumPy提供了强大的功能:
- 矢量化
- 广播
- 索引
在本教程中,你将逐步了解如何利用矢量化和广播,以便你可以充分使用NumPy。虽然你在这里将使用一些索引,但NumPy的完整索引原理图(它扩展了Python的切片语法)是它们自己的工具。如果你想了解有关NumPy索引的更多信息,请喝点咖啡,然后前往NumPy文档中的索引部分。
进入状态:介绍NumPy数组
NumPy的基本对象是它的ndarray(或numpy.array),这是一个n维数组,它也以某种形式出现在面向数组的语言中,如Fortran 90、R和MATLAB,以及以前的 APL 和 J。
让我们从形成一个包含36个元素的三维数组开始:
>>> import numpy as np
>>> arr = np.arange(36).reshape(3, 4, 3)
>>> arr
array([[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8],
[ 9, 10, 11]],
[[12, 13, 14],
[15, 16, 17],
[18, 19, 20],
[21, 22, 23]],
[[24, 25, 26],
[27, 28, 29],
[30, 31, 32],
[33, 34, 35]]])
在二维中描绘高维数组可能会比较困难。考虑数组形状的一种直观方法是简单地“从左到右读取它”。arr 是一个3乘4乘3的数组:
>>> arr.shape
(3, 4, 3)
在视觉上,arr可以被认为是三个4x3网格(或矩形棱镜)的容器,看起来像这样:
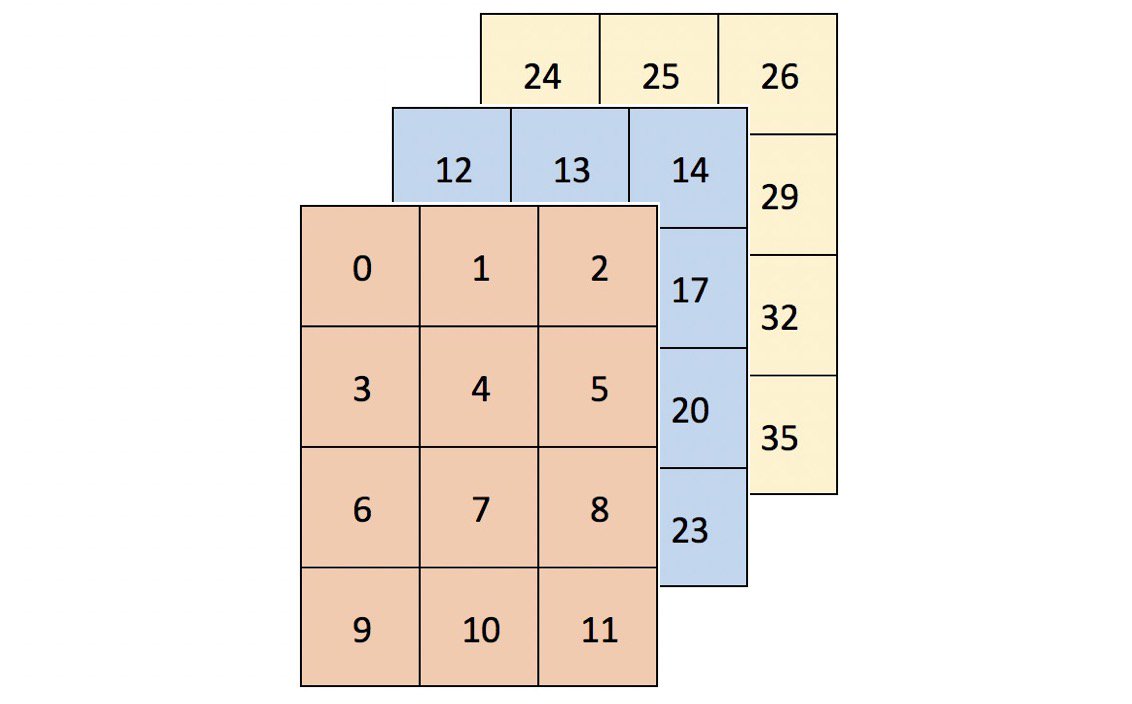
更高维度的数组可能更难以用图像表达出来,但它们仍将遵循这种“数组内的数组”模式。
你在哪里可以看到超过两个维度的数据?
- 面板数据可以用三维表示。跟踪个体群组(群体)随时间变化的数据可以被构造为(受访者,日期,属性)。 1979年全国青年纵向调查(iq调查)对27岁以上的12,686名受访者进行了调查。假设每个人每年有大约500个直接询问或派生的数据点,这些数据将具有形状(12686,27,500),总共177,604,000个数据点。
- 用于多幅图像的彩色图像数据通常存储在四个维度中。每个图像是一个三维数组(高度、宽度、通道),通道通常是红色、绿色和蓝色(RGB)值。然后,图像的集合就是(图像数、高度、宽度、通道)。1,000张256x256 RGB图像将具有形状(1000,256,256,3)。(扩展的表示是RGBA,其中A-alpha-表示不透明的级别。)。
有关高维数据的真实示例的更多详细信息,请参阅FrançoisChollet使用Python进行深度学习的第2章。
什么是矢量化?
矢量化是NumPy中的一种强大功能,可以将操作表达为在整个数组上而不是在各个元素上发生。以下是Wes McKinney的简明定义:
这种用数组表达式替换显式循环的做法通常称为向量化。通常,矢量化数组操作通常比其纯Python等价物快一个或两个(或更多)数量级,在任何类型的数值计算中都具有最大的影响。查看源码
在Python中循环数组或任何数据结构时,会涉及很多开销。 NumPy中的向量化操作将内部循环委托给高度优化的C和Fortran函数,从而实现更清晰,更快速的Python代码。
计数: 简单的如:1, 2, 3…
作为示例,考虑一个True和False的一维向量,你要为其计算序列中“False to True”转换的数量:
>>> np.random.seed(444)
>>> x = np.random.choice([False, True], size=100000)
>>> x
array([ True, False, True, ..., True, False, True])
使用Python for循环,一种方法是成对地评估序列中每个元素的真值以及紧随其后的元素:
>>> def count_transitions(x) -> int:
... count = 0
... for i, j in zip(x[:-1], x[1:]):
... if j and not i:
... count += 1
... return count
...
>>> count_transitions(x)
24984
在矢量化形式中,没有明确的for循环或直接引用各个元素:
>>> np.count_nonzero(x[:-1] < x[1:])
24984
这两个等效函数在性能方面有何比较? 在这种特殊情况下,向量化的NumPy调用胜出约70倍:
>>> from timeit import timeit
>>> setup = 'from __main__ import count_transitions, x; import numpy as np'
>>> num = 1000
>>> t1 = timeit('count_transitions(x)', setup=setup, number=num)
>>> t2 = timeit('np.count_nonzero(x[:-1] < x[1:])', setup=setup, number=num)
>>> print('Speed difference: {:0.1f}x'.format(t1 / t2))
Speed difference: 71.0x
技术细节: 另一个术语是矢量处理器,它与计算机的硬件有关。 当我在这里谈论矢量化时,我指的是用数组表达式替换显式for循环的概念,在这种情况下,可以使用低级语言在内部计算。
买低,卖高
这是另一个激发你胃口的例子。考虑以下经典技术面试问题:
假定一只股票的历史价格是一个序列,假设你只允许进行一次购买和一次出售,那么可以获得的最大利润是多少?例如,假设价格=(20,18,14,17,20,21,15),最大利润将是7,从14买到21卖。
(对所有金融界人士说:不,卖空是不允许的。)
存在具有n平方时间复杂度的解决方案,其包括采用两个价格的每个组合,其中第二价格“在第一个之后”并且确定最大差异。
然而,还有一个O(n)解决方案,它包括迭代序列一次,找出每个价格和运行最小值之间的差异。 它是这样的:
>>> def profit(prices):
... max_px = 0
... min_px = prices[0]
... for px in prices[1:]:
... min_px = min(min_px, px)
... max_px = max(px - min_px, max_px)
... return max_px
>>> prices = (20, 18, 14, 17, 20, 21, 15)
>>> profit(prices)
7
这可以用NumPy实现吗?行!没问题。但首先,让我们构建一个准现实的例子:
# Create mostly NaN array with a few 'turning points' (local min/max).
>>> prices = np.full(100, fill_value=np.nan)
>>> prices[[0, 25, 60, -1]] = [80., 30., 75., 50.]
# Linearly interpolate the missing values and add some noise.
>>> x = np.arange(len(prices))
>>> is_valid = ~np.isnan(prices)
>>> prices = np.interp(x=x, xp=x[is_valid], fp=prices[is_valid])
>>> prices += np.random.randn(len(prices)) * 2
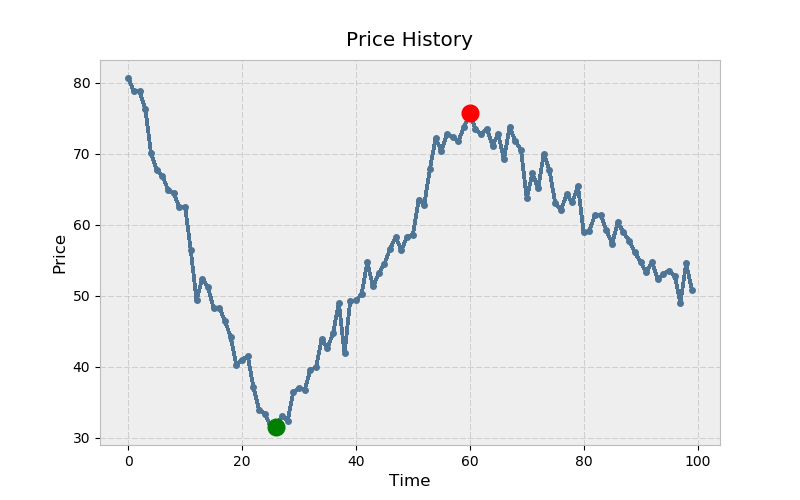
下面是matplotlib的示例。俗话说:买低(绿),卖高(红):
>>> import matplotlib.pyplot as plt
# Warning! This isn't a fully correct solution, but it works for now.
# If the absolute min came after the absolute max, you'd have trouble.
>>> mn = np.argmin(prices)
>>> mx = mn + np.argmax(prices[mn:])
>>> kwargs = {'markersize': 12, 'linestyle': ''}
>>> fig, ax = plt.subplots()
>>> ax.plot(prices)
>>> ax.set_title('Price History')
>>> ax.set_xlabel('Time')
>>> ax.set_ylabel('Price')
>>> ax.plot(mn, prices[mn], color='green', **kwargs)
>>> ax.plot(mx, prices[mx], color='red', **kwargs)
NumPy实现是什么样的? 虽然没有np.cummin() “直接”,但NumPy的通用函数(ufuncs)都有一个accumulate()方法,它的名字暗示了:
>>> cummin = np.minimum.accumulate
从纯Python示例扩展逻辑,你可以找到每个价格和运行最小值(元素方面)之间的差异,然后获取此序列的最大值:
>>> def profit_with_numpy(prices):
... """Price minus cumulative minimum price, element-wise."""
... prices = np.asarray(prices)
... return np.max(prices - cummin(prices))
>>> profit_with_numpy(prices)
44.2487532293278
>>> np.allclose(profit_with_numpy(prices), profit(prices))
True
这两个具有相同理论时间复杂度的操作如何在实际运行时进行比较? 首先,让我们采取更长的序列。(此时不一定需要是股票价格的时间序列。)
>>> seq = np.random.randint(0, 100, size=100000)
>>> seq
array([ 3, 23, 8, 67, 52, 12, 54, 72, 41, 10, ..., 46, 8, 90, 95, 93,
28, 24, 88, 24, 49])
现在,对于一个有点不公平的比较:
>>> setup = ('from __main__ import profit_with_numpy, profit, seq;'
... ' import numpy as np')
>>> num = 250
>>> pytime = timeit('profit(seq)', setup=setup, number=num)
>>> nptime = timeit('profit_with_numpy(seq)', setup=setup, number=num)
>>> print('Speed difference: {:0.1f}x'.format(pytime / nptime))
Speed difference: 76.0x
在上面,将profit_with_numpy() 视为伪代码(不考虑NumPy的底层机制),实际上有三个遍历序列:
- cummin(prices) 具有O(n)时间复杂度
- prices - cummin(prices) 是 O(n)的时间复杂度
- max(...) 是O(n)的时间复杂度
这就减少到O(n),因为O(3n)只剩下O(n)-当n接近无穷大时,n “占主导地位”。
因此,这两个函数具有等价的最坏情况时间复杂度。(不过,顺便提一下,NumPy函数的空间复杂度要高得多。)。但这可能是最不重要的内容。这里我们有一个教训是:虽然理论上的时间复杂性是一个重要的考虑因素,运行时机制也可以发挥很大的作用。NumPy不仅可以委托给C,而且通过一些元素操作和线性代数,它还可以利用多线程中的计算。但是这里有很多因素在起作用,包括所使用的底层库(BLAS/LAPACK/Atlas),而这些细节完全是另一篇文章的全部内容。
Intermezzo:理解轴符号
在NumPy中,轴指向多维数组的单个维度:
>>> arr = np.array([[1, 2, 3],
... [10, 20, 30]])
>>> arr.sum(axis=0)
array([11, 22, 33])
>>> arr.sum(axis=1)
array([ 6, 60])
围绕轴的术语和描述它们的方式可能有点不直观。在Pandas(在NumPy之上构建的库)的文档中,你可能经常看到如下内容:
axis : {'index' (0), 'columns' (1)}
根据这一描述,你可以争辩说,上面的结果应该是“反向的”。但是,关键是轴指向调用函数的轴。杰克·范德普拉斯很好地阐述了这一点:
此处指定轴的方式可能会让来自其他语言的用户感到困惑。AXIS关键字指定将折叠的数组的维度,而不是将要返回的维度。因此,指定Axis=0意味着第一个轴将折叠:对于二维数组,这意味着每列中的值将被聚合。 查看源码
换句话说,如果将AXIS=0的数组相加,则会使用按列计算的方式折叠数组的行。
考虑到这一区别,让我们继续探讨广播的概念。
广播
广播是另一个重要的NumPy抽象。你已经看到了两个NumPy数组(大小相等)之间的操作是按元素操作的:
>>> a = np.array([1.5, 2.5, 3.5])
>>> b = np.array([10., 5., 1.])
>>> a / b
array([0.15, 0.5 , 3.5 ])
但是,大小不相等的数组呢?这就是广播的意义所在:
术语广播描述了在算术运算期间NumPy如何处理具有不同形状的数组。受某些约束条件的限制,较小的数组会在较大的数组中“广播”,以便它们具有兼容的形状。广播提供了一种向量化数组操作的方法,因此循环是在C而不是Python中进行的。查看源码
当使用两个以上的数组时,广播的实现方式可能会变得乏味。但是,如果只有两个数组,那么可以用两条简短的规则来描述它们的广播能力:
在对两个数组进行操作时,NumPy按元素对它们的形状进行比较。它从尾随维度开始,然后继续前进。两个维度在下列情况下是兼容的: - 他们是平等的,或者 - 其中一个是1
非那样做不行。
让我们以一个例子为例,我们想要减去数组的每个列的平均值,元素的平均值:
>>> sample = np.random.normal(loc=[2., 20.], scale=[1., 3.5],
... size=(3, 2))
>>> sample
array([[ 1.816 , 23.703 ],
[ 2.8395, 12.2607],
[ 3.5901, 24.2115]])
在统计术语中,样本由两个独立于两个总体的样本(列)组成,平均值分别为2和20。按列分列的方法应该近似于总体方法(尽管是粗略的,因为样本很小):
>>> mu = sample.mean(axis=0)
>>> mu
array([ 2.7486, 20.0584])
现在,减去列意义是很简单的,因为广播规则检查出来了:
>>> print('sample:', sample.shape, '| means:', mu.shape)
sample: (3, 2) | means: (2,)
>>> sample - mu
array([[-0.9325, 3.6446],
[ 0.091 , -7.7977],
[ 0.8416, 4.1531]])
下面是一个减去列意义的示例,其中较小的数组被“拉伸”,以便从较大的数组的每一行中减去它:
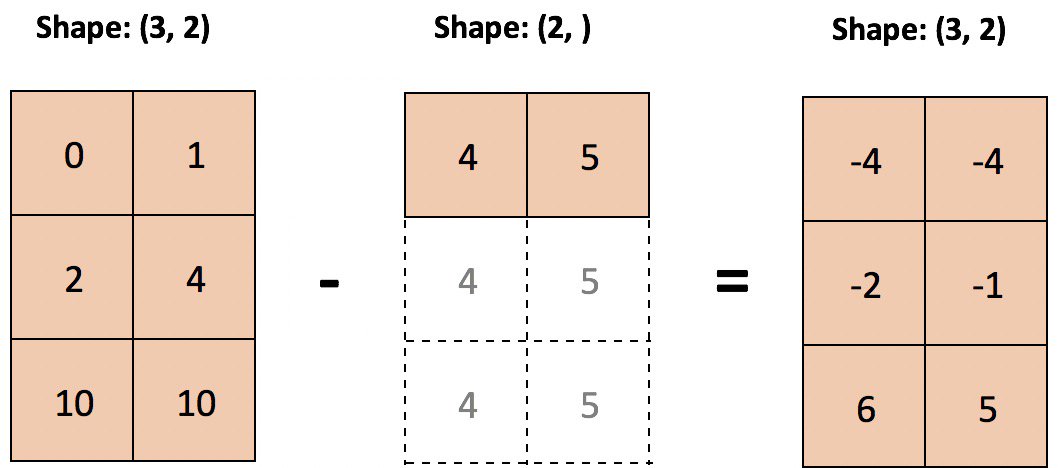
技术细节:较小的数组或标量不是按字面意义上在内存中展开的:重复的是计算本身。
这扩展到标准化每个列,使每个单元格相对于其各自的列具有z-score:
>>> (sample - sample.mean(axis=0)) / sample.std(axis=0)
array([[-1.2825, 0.6605],
[ 0.1251, -1.4132],
[ 1.1574, 0.7527]])
但是,如果出于某种原因,要减去行最小值,该怎么办?你会遇到这样的麻烦:
>>> sample - sample.min(axis=1)
ValueError: operands could not be broadcast together with shapes (3,2) (3,)
这里的问题是,较小的数组,在其目前的形式,不能“伸展”,以形状与样本兼容。实际上,你需要扩展它的维度,以满足上面的广播规则:
>>> sample.min(axis=1)[:, None] # 3 minimums across 3 rows
array([[1.816 ],
[2.8395],
[3.5901]])
>>> sample - sample.min(axis=1)[:, None]
array([[ 0. , 21.887 ],
[ 0. , 9.4212],
[ 0. , 20.6214]])
注意: [:, None]是一种扩展数组维度的方法,用于创建长度为1的轴。np.newaxis是None的别名。
还有一些更为复杂的案例。下面是任何形状的任意数量的数组可以一起广播的更严格的定义:
如果以下规则产生有效结果,则一组数组被称为“可广播”到相同的形状,这意味着 以下之一为真 时: 1. 矩阵都具有完全相同的形状。 1. 矩阵都具有相同数量的维度,每个维度的长度是公共长度或1。 1. 具有太少尺寸的矩列可以使其形状前面具有长度为1的尺寸以满足属性#2。 查看源码
这更容易一步一步走。假设你有以下四个数组:
>>> a = np.sin(np.arange(10)[:, None])
>>> b = np.random.randn(1, 10)
>>> c = np.full_like(a, 10)
>>> d = 8
在检查形状之前,NumPy首先将标量转换为具有一个元素的数组:
>>> arrays = [np.atleast_1d(arr) for arr in (a, b, c, d)]
>>> for arr in arrays:
... print(arr.shape)
...
(10, 1)
(1, 10)
(10, 1)
(1,)
现在我们可以检查标准#1。如果所有数组具有相同的形状,则它们的一组形状将缩减为一个元素,因为set() 构造函数有效地从其输入中删除重复项。这里显然没有达到这个标准:
>>> len(set(arr.shape for arr in arrays)) == 1
False
标准#2的第一部分也失败了,这意味着整个标准失败:
>>> len(set((arr.ndim) for arr in arrays)) == 1
False
最后一个标准更复杂一些:
具有太少尺寸的矩列可以使其形状前面具有长度为1的尺寸以满足属性#2。
为了对此进行编码,你可以首先确定最高维数组的维度,然后将其添加到每个形状元组,直到所有数组具有相同的维度:
>>> maxdim = max(arr.ndim for arr in arrays) # Maximum dimensionality
>>> shapes = np.array([(1,) * (maxdim - arr.ndim) + arr.shape
... for arr in arrays])
>>> shapes
array([[10, 1],
[ 1, 10],
[10, 1],
[ 1, 1]])
最后,你需要测试每个维度的长度是否是公共长度,或是1。这样做的一个技巧是首先在“等于”的位置屏蔽“shape-tuples”数组。然后,你可以检查 peak-to-peak(np.ptp())列方差是否都为零:
>>> masked = np.ma.masked_where(shapes == 1, shapes)
>>> np.all(masked.ptp(axis=0) == 0) # ptp: max - min
True
这个逻辑封装在单个函数中,如下所示:
>>> def can_broadcast(*arrays) -> bool:
... arrays = [np.atleast_1d(arr) for arr in arrays]
... if len(set(arr.shape for arr in arrays)) == 1:
... return True
... if len(set((arr.ndim) for arr in arrays)) == 1:
... return True
... maxdim = max(arr.ndim for arr in arrays)
... shapes = np.array([(1,) * (maxdim - arr.ndim) + arr.shape
... for arr in arrays])
... masked = np.ma.masked_where(shapes == 1, shapes)
... return np.all(masked.ptp(axis=0) == 0)
...
>>> can_broadcast(a, b, c, d)
True
幸运的是,你可以选择一个快捷方式并使用np.cast()来进行这种健全性检查,尽管它并不是为此目的而显式设计的:
>>> def can_broadcast(*arrays) -> bool:
... try:
... np.broadcast(*arrays)
... return True
... except ValueError:
... return False
...
>>> can_broadcast(a, b, c, d)
True
对于那些有兴趣深入挖掘的人来说,PyArray_Broadcast是封装广播规则的底层C函数。
矩阵编程实际应用:示例
在以下3个示例中,你将使用矢量化和广播来处理一些实际应用程序。
聚类算法
机器学习是一个可以经常利用矢量化和广播的领域。 假设你有三角形的顶点(每行是x,y坐标):
>>> tri = np.array([[1, 1],
... [3, 1],
... [2, 3]])
这个“簇”的质心是(x, y)坐标,它是每列的算术平均值:
>>> centroid = tri.mean(axis=0)
>>> centroid
array([2. , 1.6667])
可视化这有助于:
>>> trishape = plt.Polygon(tri, edgecolor='r', alpha=0.2, lw=5)
>>> _, ax = plt.subplots(figsize=(4, 4))
>>> ax.add_patch(trishape)
>>> ax.set_ylim([.5, 3.5])
>>> ax.set_xlim([.5, 3.5])
>>> ax.scatter(*centroid, color='g', marker='D', s=70)
>>> ax.scatter(*tri.T, color='b', s=70)
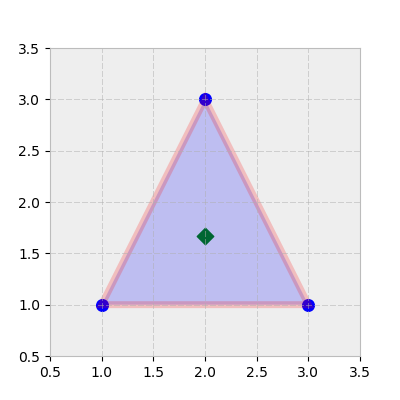
许多聚类算法利用点集合的欧几里德距离,或者指向原点,或者相对于它们的质心。
在笛卡尔坐标下,p点和q点之间的欧几里德距离是:
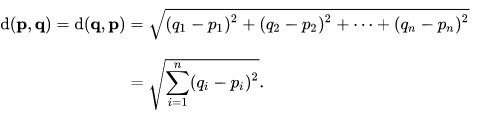
[查看源码]
因此,对于上面的三坐标集,每个点到原点(0, 0) 的欧几里德距离是:
>>> np.sum(tri**2, axis=1) ** 0.5 # Or: np.sqrt(np.sum(np.square(tri), 1))
array([1.4142, 3.1623, 3.6056])
你可能会认识到我们实际上只是在寻找附和欧几里德的规则:
>>> np.linalg.norm(tri, axis=1)
array([1.4142, 3.1623, 3.6056])
你也可以找到相对于三角形质心的每个点的范数,而不是参考原点:
>>> np.linalg.norm(tri - centroid, axis=1)
array([1.2019, 1.2019, 1.3333])
最后,让我们更进一步:假设你有一个二维数组X和一个多个(x, y) “建议”质心的二维数组。诸如K-Means聚类的算法)通过随机分配初始“建议”质心,然后将每个数据点重新分配到其最接近的质心来工作。从那里开始,计算新的质心,一旦重新生成的标签(质心的编码)在迭代之间不变,算法就会收敛于解。这个个迭代过程的一部分需要计算每个质心中每个点的欧几里德距离:
>>> X = np.repeat([[5, 5], [10, 10]], [5, 5], axis=0)
>>> X = X + np.random.randn(*X.shape) # 2 distinct "blobs"
>>> centroids = np.array([[5, 5], [10, 10]])
>>> X
array([[ 3.3955, 3.682 ],
[ 5.9224, 5.785 ],
[ 5.9087, 4.5986],
[ 6.5796, 3.8713],
[ 3.8488, 6.7029],
[10.1698, 9.2887],
[10.1789, 9.8801],
[ 7.8885, 8.7014],
[ 8.6206, 8.2016],
[ 8.851 , 10.0091]])
>>> centroids
array([[ 5, 5],
[10, 10]])
换句话说,我们想回答这个问题,X中的每个点所属的质心是什么? 为了计算X中每个点与质心中每个点之间的欧几里德距离,我们需要进行一些重构以在此处启用广播:
>>> centroids[:, None]
array([[[ 5, 5]],
[[10, 10]]])
>>> centroids[:, None].shape
(2, 1, 2)
这使我们能够使用一个数组行的组合乘积,从另一个数组中清清楚楚地减掉这些数组:
>>> np.linalg.norm(X - centroids[:, None], axis=2).round(2)
array([[2.08, 1.21, 0.99, 1.94, 2.06, 6.72, 7.12, 4.7 , 4.83, 6.32],
[9.14, 5.86, 6.78, 7.02, 6.98, 0.73, 0.22, 2.48, 2.27, 1.15]])
换句话说,X-质心[:, None]的形状是(2,10,2),本质上表示两个堆叠的数组,每个数组的大小都为X。接下来,我们希望每个最近的质心的标签(索引号),从上面的数组找出第0轴上的最小距离:
>>> np.argmin(np.linalg.norm(X - centroids[:, None], axis=2), axis=0)
array([0, 0, 0, 0, 0, 1, 1, 1, 1, 1])
你可以将所有这些以函数形式组合在一起:
>>> def get_labels(X, centroids) -> np.ndarray:
... return np.argmin(np.linalg.norm(X - centroids[:, None], axis=2),
... axis=0)
>>> labels = get_labels(X, centroids)
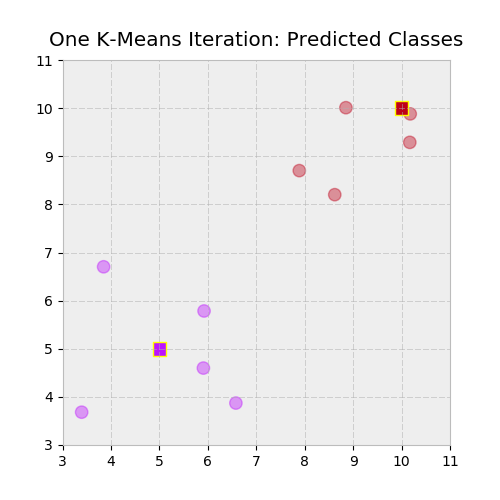
让我们来直观地检查一下,用一个颜色映射来绘制两个集群和它们指定的标签:
>>> c1, c2 = ['#bc13fe', '#be0119'] # https://xkcd.com/color/rgb/
>>> llim, ulim = np.trunc([X.min() * 0.9, X.max() * 1.1])
>>> _, ax = plt.subplots(figsize=(5, 5))
>>> ax.scatter(*X.T, c=np.where(labels, c2, c1), alpha=0.4, s=80)
>>> ax.scatter(*centroids.T, c=[c1, c2], marker='s', s=95,
... edgecolor='yellow')
>>> ax.set_ylim([llim, ulim])
>>> ax.set_xlim([llim, ulim])
>>> ax.set_title('One K-Means Iteration: Predicted Classes')
摊还(分期)表
矢量化也适用于金融领域。
给定年利率,支付频率(每年的次数),初始贷款余额和贷款期限,你可以以矢量化方式创建包含月贷款余额和付款的摊还表。让我们先设置一些标量常量:
>>> freq = 12 # 12 months per year
>>> rate = .0675 # 6.75% annualized
>>> nper = 30 # 30 years
>>> pv = 200000 # Loan face value
>>> rate /= freq # Monthly basis
>>> nper *= freq # 360 months
NumPy预装了一些财务函数,与Excel表兄弟不同,它们能够以矢量的形式输出。
债务人(或承租人)每月支付一笔由本金和利息部分组成的固定金额。由于未偿还的贷款余额下降,总付款的利息部分随之下降。
>>> periods = np.arange(1, nper + 1, dtype=int)
>>> principal = np.ppmt(rate, periods, nper, pv)
>>> interest = np.ipmt(rate, periods, nper, pv)
>>> pmt = principal + interest # Or: pmt = np.pmt(rate, nper, pv)
接下来,你需要计算每月的余额,包括支付前和付款后的余额,可以定义为原始余额的未来价值减去年金(支付流)的未来价值,使用折扣因子d:
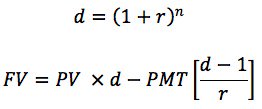
从功能上看,如下所示:
>>> def balance(pv, rate, nper, pmt) -> np.ndarray:
... d = (1 + rate) ** nper # Discount factor
... return pv * d - pmt * (d - 1) / rate
最后,你可以使用Pandas 的 DataFrame 将其放到表格格式中。小心这里的标志。从债务人的角度看,PMT是一种流出。
>>> import pandas as pd
>>> cols = ['beg_bal', 'prin', 'interest', 'end_bal']
>>> data = [balance(pv, rate, periods - 1, -pmt),
... principal,
... interest,
... balance(pv, rate, periods, -pmt)]
>>> table = pd.DataFrame(data, columns=periods, index=cols).T
>>> table.index.name = 'month'
>>> with pd.option_context('display.max_rows', 6):
... # Note: Using floats for $$ in production-level code = bad
... print(table.round(2))
...
beg_bal prin interest end_bal
month
1 200000.00 -172.20 -1125.00 199827.80
2 199827.80 -173.16 -1124.03 199654.64
3 199654.64 -174.14 -1123.06 199480.50
... ... ... ... ...
358 3848.22 -1275.55 -21.65 2572.67
359 2572.67 -1282.72 -14.47 1289.94
360 1289.94 -1289.94 -7.26 -0.00
At the end of year 30, the loan is paid off:
>>> final_month = periods[-1]
>>> np.allclose(table.loc[final_month, 'end_bal'], 0)
True
注意: 虽然使用浮点数代表资金对于脚本环境中的概念说明非常有用,但在生产环境中使用Python浮点数进行财务计算可能会导致计算在某些情况下损失一两分钱。
图像特征提取
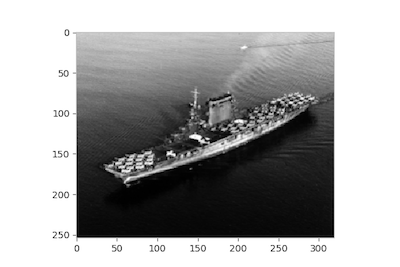
在最后一个例子中,我们将处理1941年10月莱克星顿号航空母舰(CV-2)的照片,这艘船的残骸是2018年3月在澳大利亚海岸外发现的。首先,我们可以将图像映射到它的像素值的NumPy数组中:
>>> from skimage import io
>>> url = ('https://www.history.navy.mil/bin/imageDownload?image=/'
... 'content/dam/nhhc/our-collections/photography/images/'
... '80-G-410000/80-G-416362&rendition=cq5dam.thumbnail.319.319.png')
>>> img = io.imread(url, as_grey=True)
>>> fig, ax = plt.subplots()
>>> ax.imshow(img, cmap='gray')
>>> ax.grid(False)
为了简单起见,图像是以灰度加载的,结果是一个由64位浮点数组成的2d数组,而不是一个三维mxnx4rgba数组,更低的值表示暗点:
>>> img.shape
(254, 319)
>>> img.min(), img.max()
(0.027450980392156862, 1.0)
>>> img[0, :10] # First ten cells of the first row
array([0.8078, 0.7961, 0.7804, 0.7882, 0.7961, 0.8078, 0.8039, 0.7922,
0.7961, 0.7961])
>>> img[-1, -10:] # Last ten cells of the last row
array([0.0784, 0.0784, 0.0706, 0.0706, 0.0745, 0.0706, 0.0745, 0.0784,
0.0784, 0.0824])
在图像分析中,一种常用的中间步骤是贴片提取。顾名思义,这包括从较大的数组中提取较小的重叠子数组,并可用于有利于“去噪”或模糊图像的情况。
这一概念也扩展到其他领域。例如,你可以通过使用具有多个特性(变量)的时间序列的“滚动”窗口来做类似的事情。它甚至对构建康威的“生命游戏”很有用。(不过,与3x3内核的卷积是一种更直接的方法。)
在这里,我们将找到 img 中每个重叠的10x10修补的平均值。以一个微型示例为例,img左上角的第一个3x3修补程序矩阵将是:
>>> img[:3, :3]
array([[0.8078, 0.7961, 0.7804],
[0.8039, 0.8157, 0.8078],
[0.7882, 0.8 , 0.7961]])
>>> img[:3, :3].mean()
0.7995642701525054
用于创建滑动修复方式的纯Python方法将涉及嵌套的for循环。你需要考虑最右边补丁的起始索引是在索引 n - 3 + 1,其中n是数组的宽度。换句话说,如果你从名为arr的10x10数组中提取3x3修复,那么最后一个修复将来自arr[7: 10, 7: 10]。 还要记住,Python的range()不包含其stop参数:
>>> size = 10
>>> m, n = img.shape
>>> mm, nn = m - size + 1, n - size + 1
>>>
>>> patch_means = np.empty((mm, nn))
>>> for i in range(mm):
... for j in range(nn):
... patch_means[i, j] = img[i: i+size, j: j+size].mean()
>>> fig, ax = plt.subplots()
>>> ax.imshow(patch_means, cmap='gray')
>>> ax.grid(False)
有了这个循环,你就会执行很多Python调用。
另一种可扩展到更大RGB或RGBA图像的替代方案是NumPy的stride_tricks。
一个有益的第一步是在给定修补大小和图像形状的情况下,可视化更高维度的修复矩阵。我们有一个2d数组img形状(254, 319)和一个(10, 10)2d 修复。这意味着我们的输出形状(在取每个“内部” 10x10 数组的平均值之前)将是:
>>> shape = (img.shape[0] - size + 1, img.shape[1] - size + 1, size, size)
>>> shape
(245, 310, 10, 10)
你还需要指定新数组的步长。数组的步长是一个字节元组,用于在沿数组移动时跳转到每个维度。IMG中的每个像素都是64位(8字节)的浮点,这意味着总的图像大小为254×319×8 = 648, 208字节。
>>> img.dtype
dtype('float64')
>>> img.nbytes
648208
在内部,IMG作为一个连续的648,208字节块保存在内存中。因此,STEAMS是一种类似“元数据”的属性,它告诉我们需要向前跳转多少字节才能沿着每个轴移动到下一个位置。我们沿着行以8字节为单位移动,但需要遍历8x319=2,552字节才能将“向下”从一行移动到另一行。
>>> img.strides
(2552, 8)
在我们的示例中,生成的修复程序的步调只会重复img的两次步调:
>>> strides = 2 * img.strides
>>> strides
(2552, 8, 2552, 8)
现在,让我们将这些部分与NumPy的stride_tricks结合起来:
>>> from numpy.lib import stride_tricks
>>> patches = stride_tricks.as_strided(img, shape=shape, strides=strides)
>>> patches.shape
(245, 310, 10, 10)
Here’s the first 10x10 patch:
>>> patches[0, 0].round(2)
array([[0.81, 0.8 , 0.78, 0.79, 0.8 , 0.81, 0.8 , 0.79, 0.8 , 0.8 ],
[0.8 , 0.82, 0.81, 0.79, 0.79, 0.79, 0.78, 0.81, 0.81, 0.8 ],
[0.79, 0.8 , 0.8 , 0.79, 0.8 , 0.8 , 0.82, 0.83, 0.79, 0.81],
[0.8 , 0.79, 0.81, 0.81, 0.8 , 0.8 , 0.78, 0.76, 0.8 , 0.79],
[0.78, 0.8 , 0.8 , 0.78, 0.8 , 0.79, 0.78, 0.78, 0.79, 0.79],
[0.8 , 0.8 , 0.78, 0.78, 0.78, 0.8 , 0.8 , 0.8 , 0.81, 0.79],
[0.78, 0.77, 0.78, 0.76, 0.77, 0.8 , 0.8 , 0.77, 0.8 , 0.8 ],
[0.79, 0.76, 0.77, 0.78, 0.77, 0.77, 0.79, 0.78, 0.77, 0.76],
[0.78, 0.75, 0.76, 0.76, 0.73, 0.75, 0.78, 0.76, 0.77, 0.77],
[0.78, 0.79, 0.78, 0.78, 0.78, 0.78, 0.77, 0.76, 0.77, 0.77]])
最后一步很棘手。 为了得到每个内部10x10数组的矢量化平均值,我们需要仔细考虑我们现在拥有的维数。结果应该折叠最后两个维度,以便我们留下一个245x310数组。
一种(次优)方式是首先重塑修复,将内部2d数组展平为长度为100的向量,然后计算最终轴上的均值:
>>> veclen = size ** 2
>>> patches.reshape(*patches.shape[:2], veclen).mean(axis=-1).shape
(245, 310)
但是,你也可以将轴指定为元组,计算最后两个轴的平均值,这应该比重新整形更有效:
>>> patches.mean(axis=(-1, -2)).shape
(245, 310)
让我们通过比较与循环版本的相等性来确保检查。它确实如下:
>>> strided_means = patches.mean(axis=(-1, -2))
>>> np.allclose(patch_means, strided_means)
True
如果大步幅的概念让你感到兴奋,请不要激动:Scikit-Learn已经在其feature_extraction模块中很好地嵌入了整个过程。
临别赠言:不要过度优化
在本文中,我们讨论了利用NumPy中的数组编程来优化运行时。在处理大型数据集时,注意微观性能非常重要。
但是,有一部分案例无法避免使用本机Python for循环。正如Donald Knuth所说,“过早优化是所有邪恶的根源。”程序员可能错误地预测他们的代码中会出现瓶颈的地方,花费数小时试图完全矢量化操作,这将导致运行时相对不显着的改进。
在这里或那里都放上for循环也没有任何问题。通常,考虑在更高的抽象级别优化整个脚本的流程和结构,可能会更有效率。
更多资源
免费奖励:单击此处可获得免费的NumPy资源指南,该指南将为你提供提高NumPy技能的最佳教程、视频和书籍。
NumPy 文档:
书籍:
- Travis Oliphant’s Guide to NumPy, 2nd ed. (特拉维斯是NumPy的主要创建者。)
- Chapter 2 (“Introduction to NumPy”) of Jake VanderPlas’ Python数据科学手册
- Chapter 4 (“NumPy Basics”) and Chapter 12 (“Advanced NumPy”) of Wes McKinney’s Python for Data Analysis 2nd ed.
- Chapter 2 (“The Mathematical Building Blocks of Neural Networks”) from François Chollet’s Deep Learning with Python
- Robert Johansson’s Numerical Python
- Ivan Idris: Numpy Beginner’s Guide, 3rd ed.
其他资源:
- 维基百科: 数组编程
- SciPy 课堂讲义: Basic and Advanced NumPy
- EricsBroadcastingDoc: NumPy中的数组广播
- SciPy Cookbook: NumPy中的视图与副本
- Nicolas Rougier: 从Python到Numpy and 100 NumPy练习
- TensorFlow 文档: 广播语法
- Theano 文档: 广播
- Eli Bendersky: 用Numpy广播数组
文章出处
由NumPy中文文档翻译,原作者为 Brad Solomon,翻译至:https://realpython.com/numpy-array-programming/